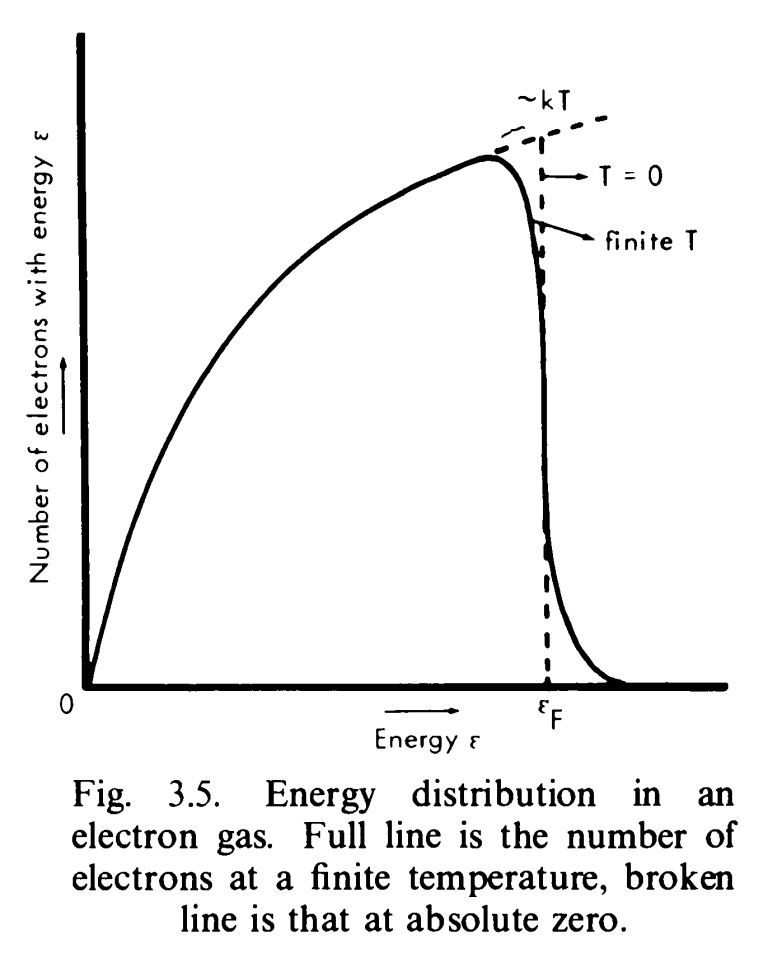
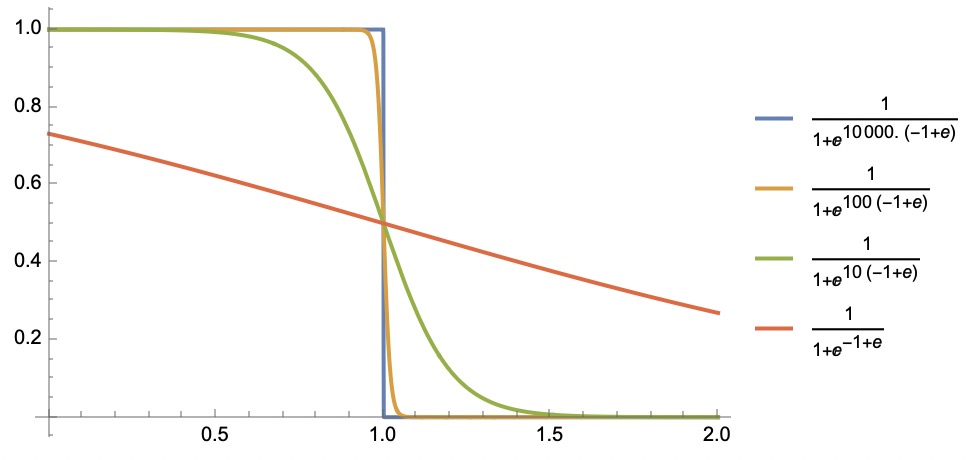
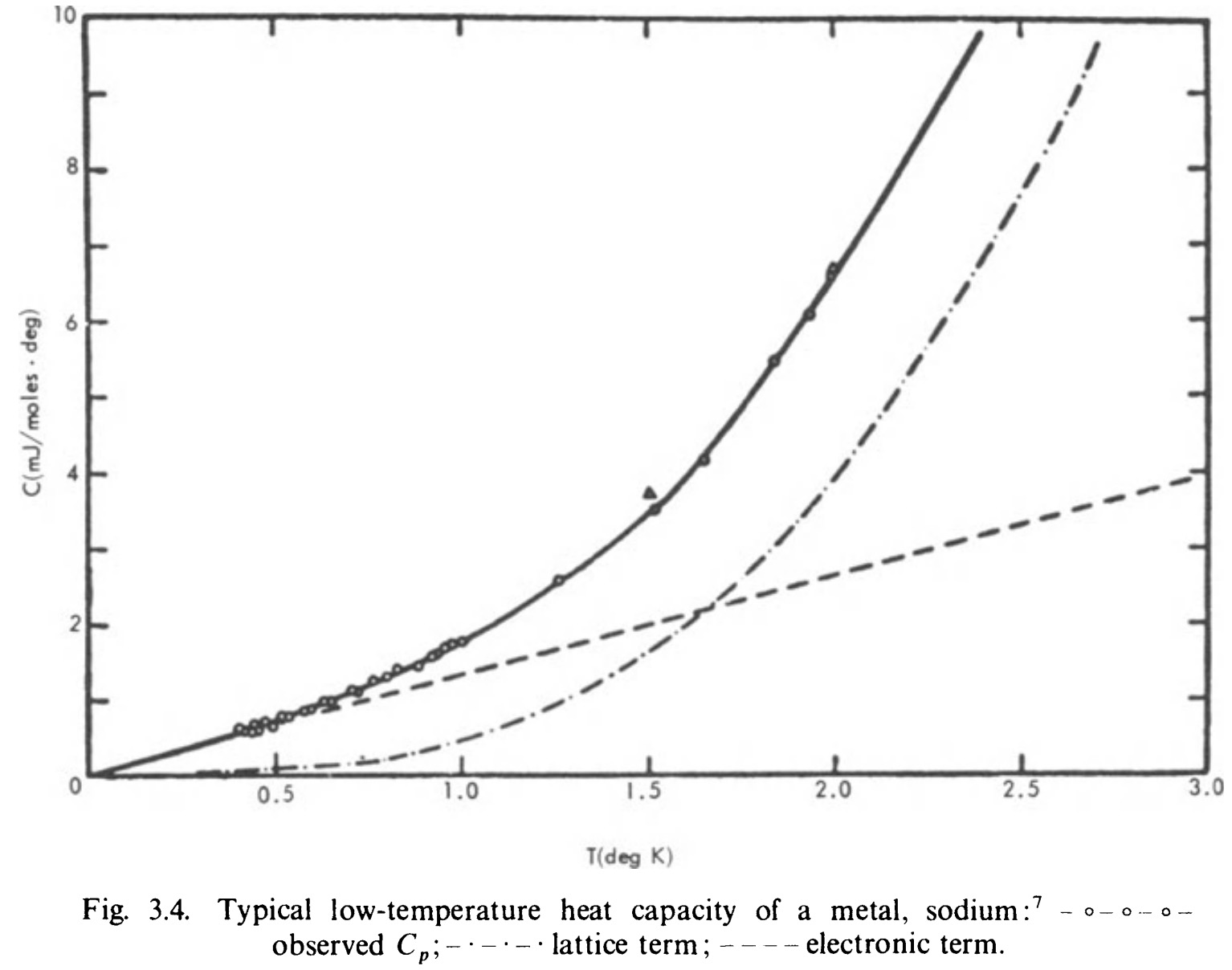
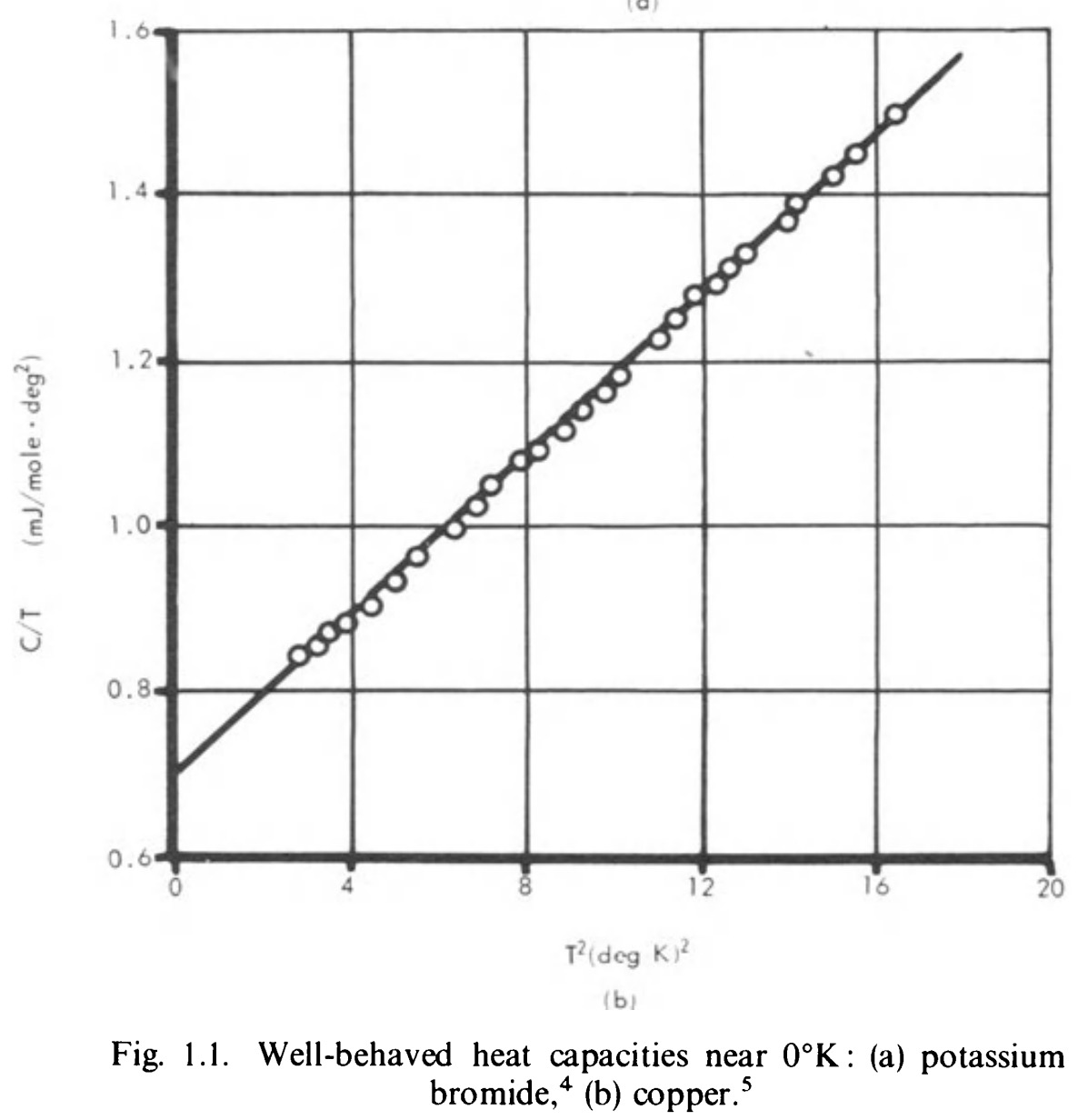
A theory is the more impressive the greater the simplicity of its premises, the more different kinds of things it relates, and the more extended its area of applicability. Therefore the deep impression that classical thermodynamics made upon me. It is the only physical theory of universal content which I am convinced will never be overthrown, within the framework of applicability of its basic concepts.
上邪!我欲与君相知,长命无绝衰。
山无陵,江水为竭,冬雷震震,夏雨雪,天地合,乃敢与君绝!
热律!熵增不可逆,时空永无衰。
热自冰传火,气自聚成埃,老返童,水归山,机永动,乃敢言此律乖!
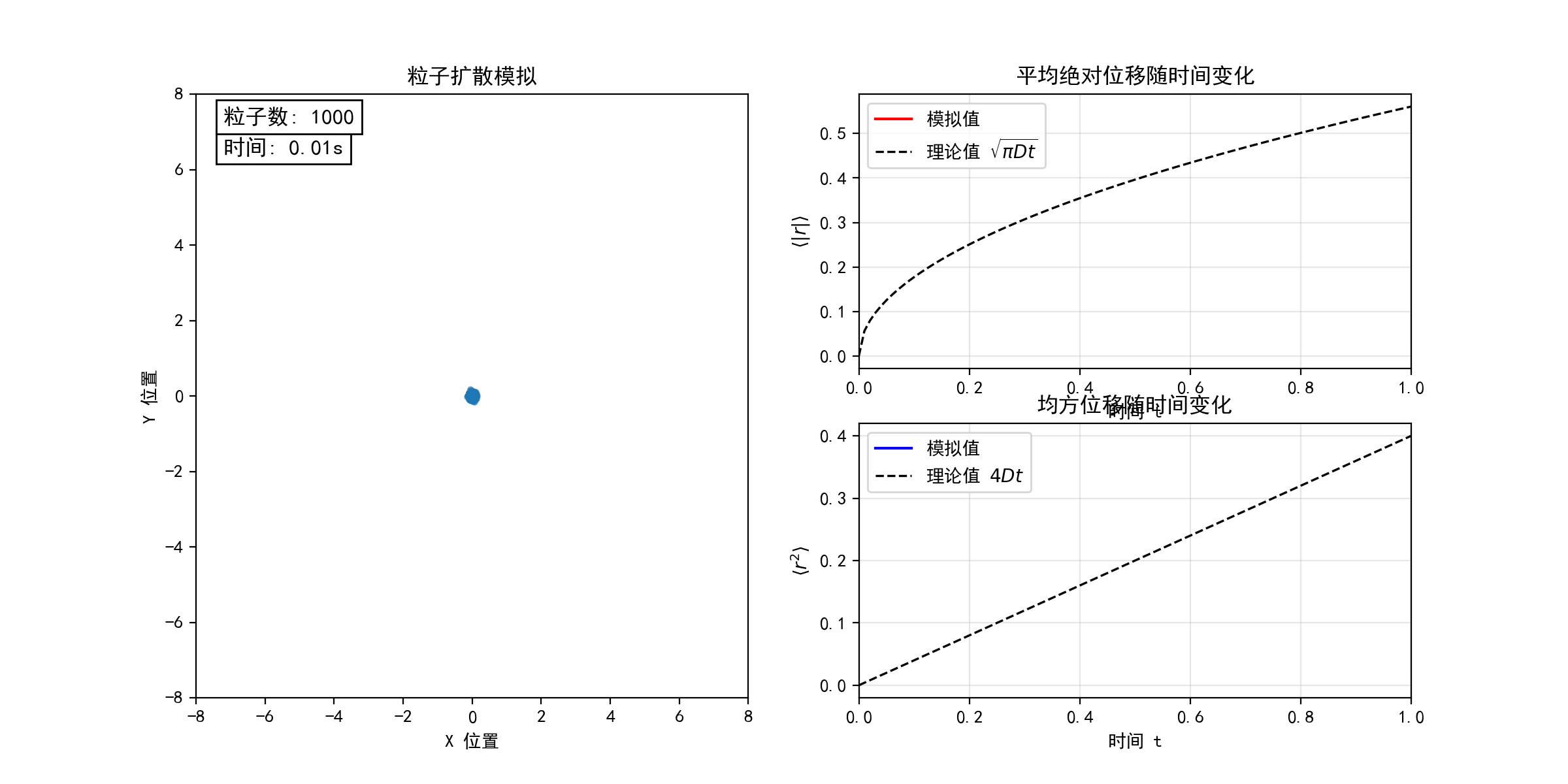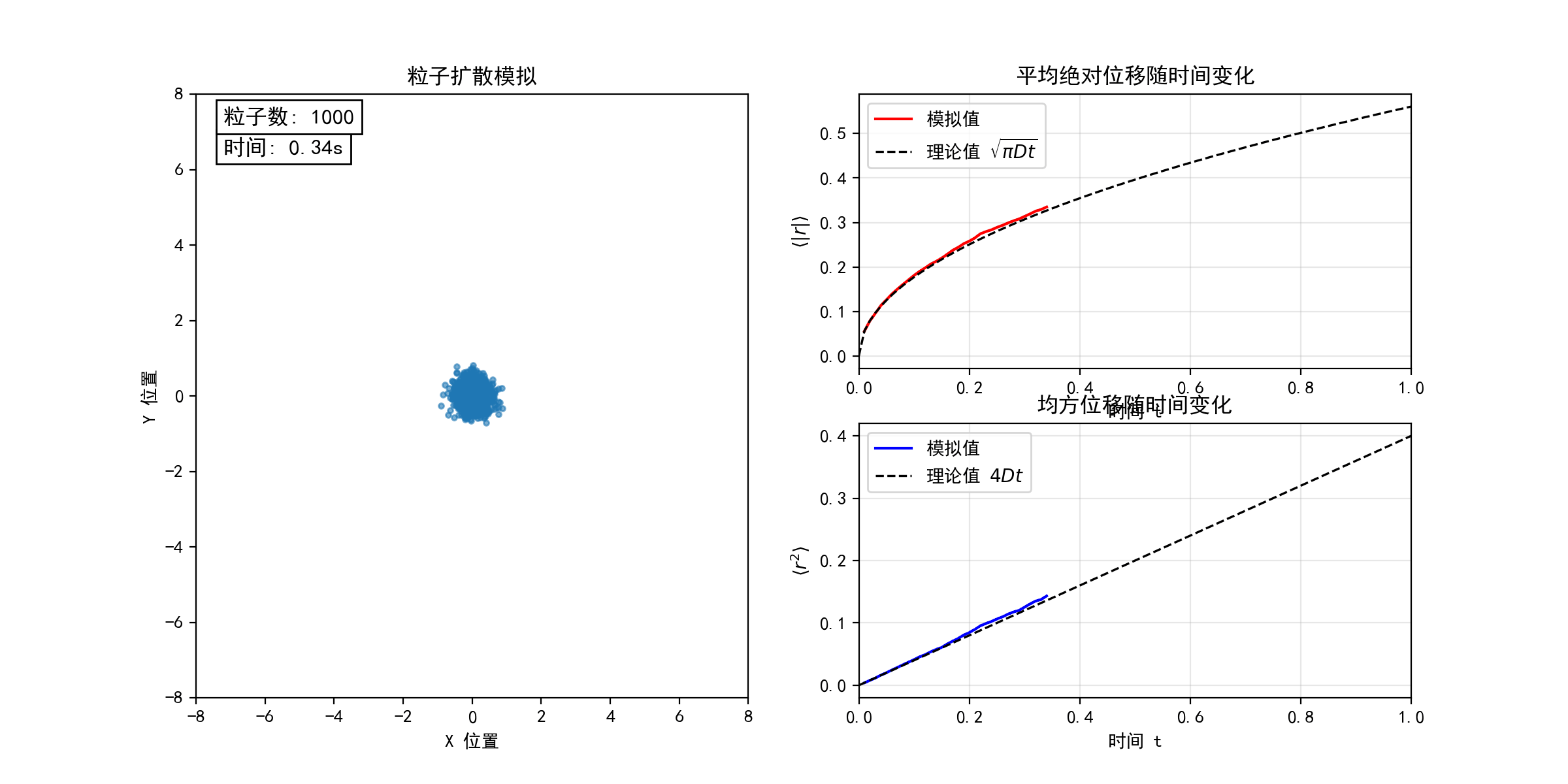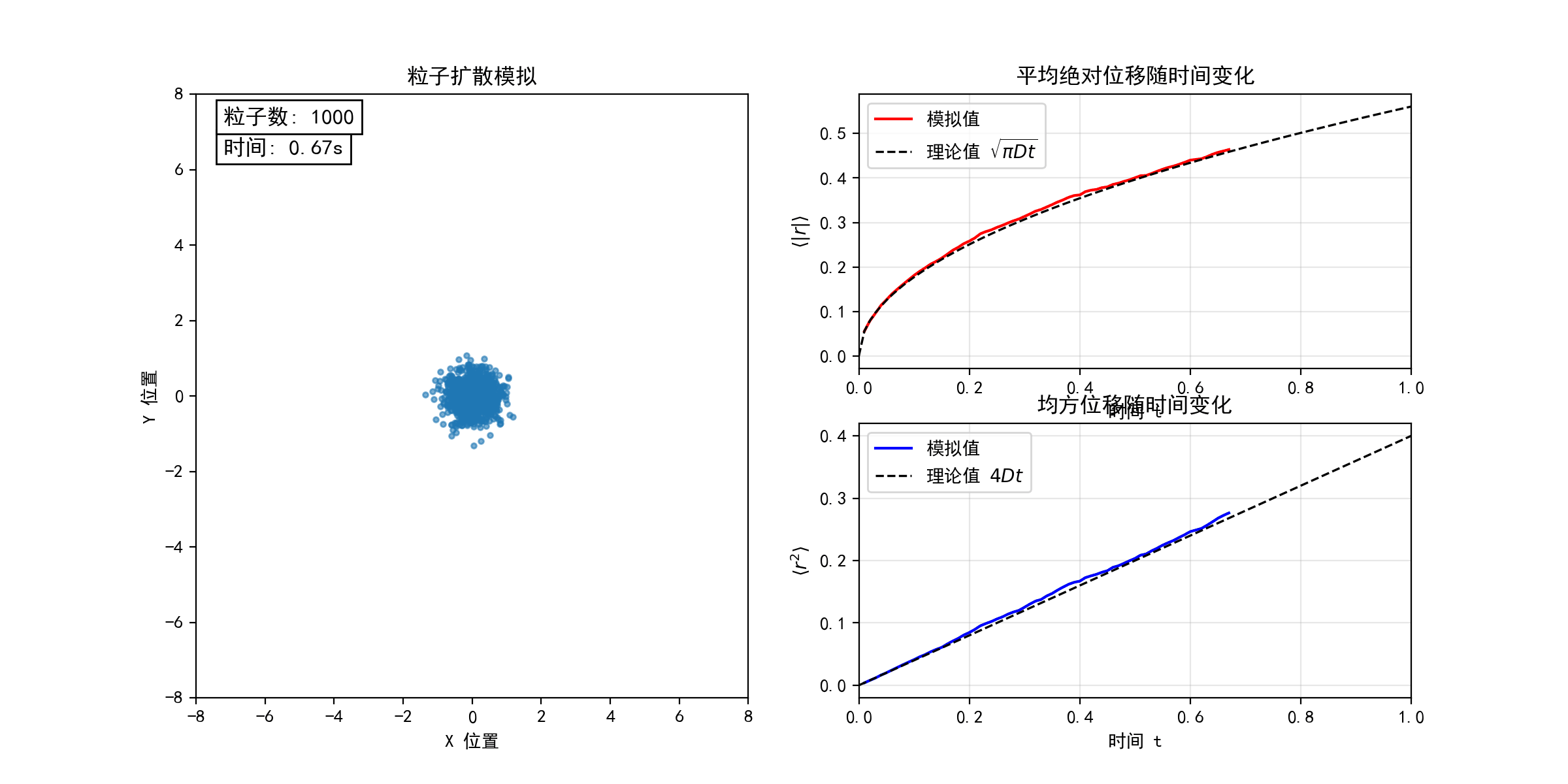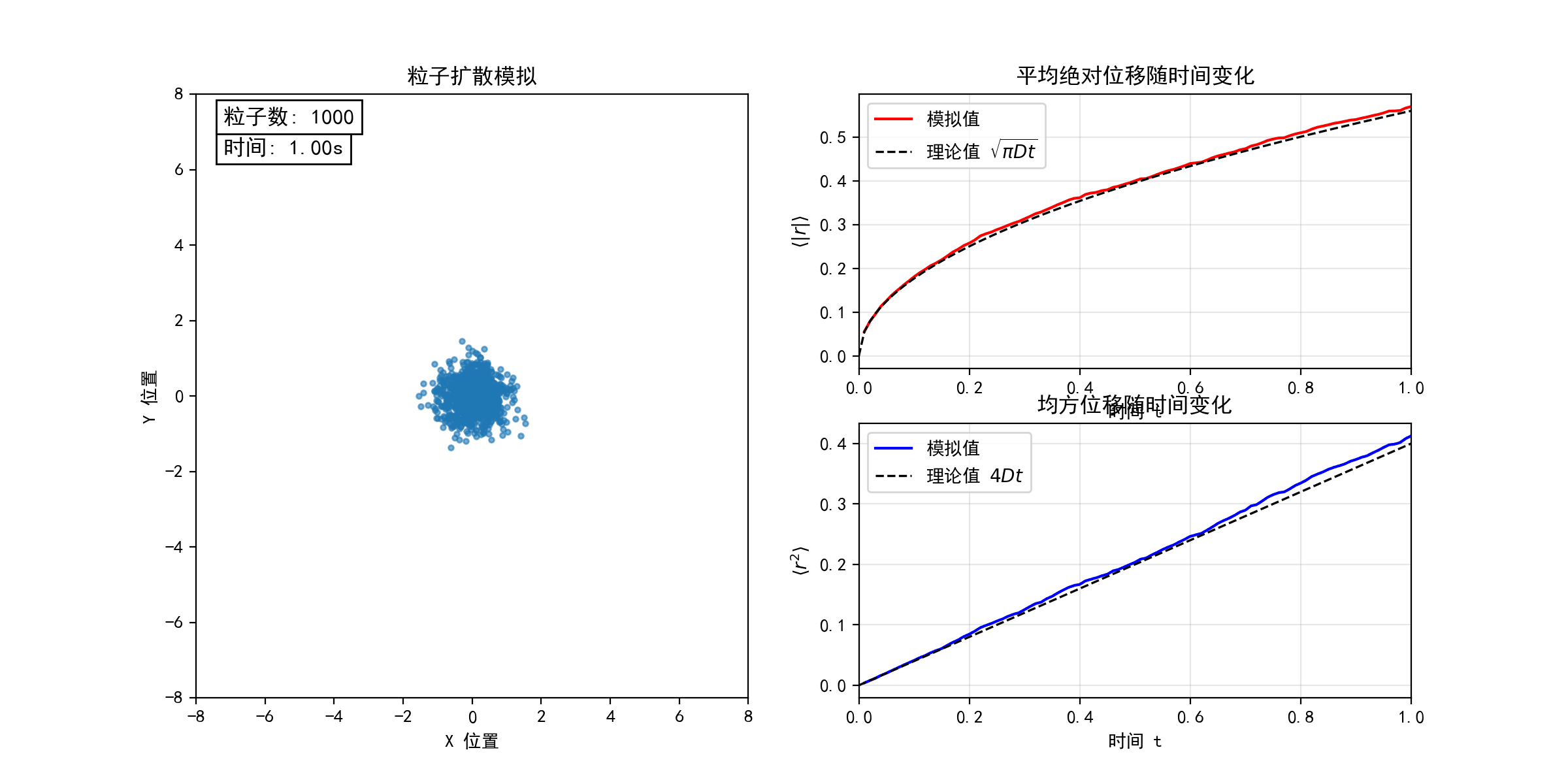
考虑二维平面上的随机游走模型(醉汉行走问题)。每个粒子从坐标原点出发,以等概率向四个基本方向(上、下、左、右)随机运动。下图模拟了不同粒子数目(N = 10, 100, 1000)的随机游走过程,宏观上表现为粒子的扩散行为。在连续极限下,粒子数密度分布函数 满足经典的扩散方程
。随着粒子数目N的增加,粒子的位移和均方位移的统计平均值均逐渐收敛于扩散方程的解(图中虚线所示),验证了微观随机过程与宏观扩散现象的联系。(python代码下载)
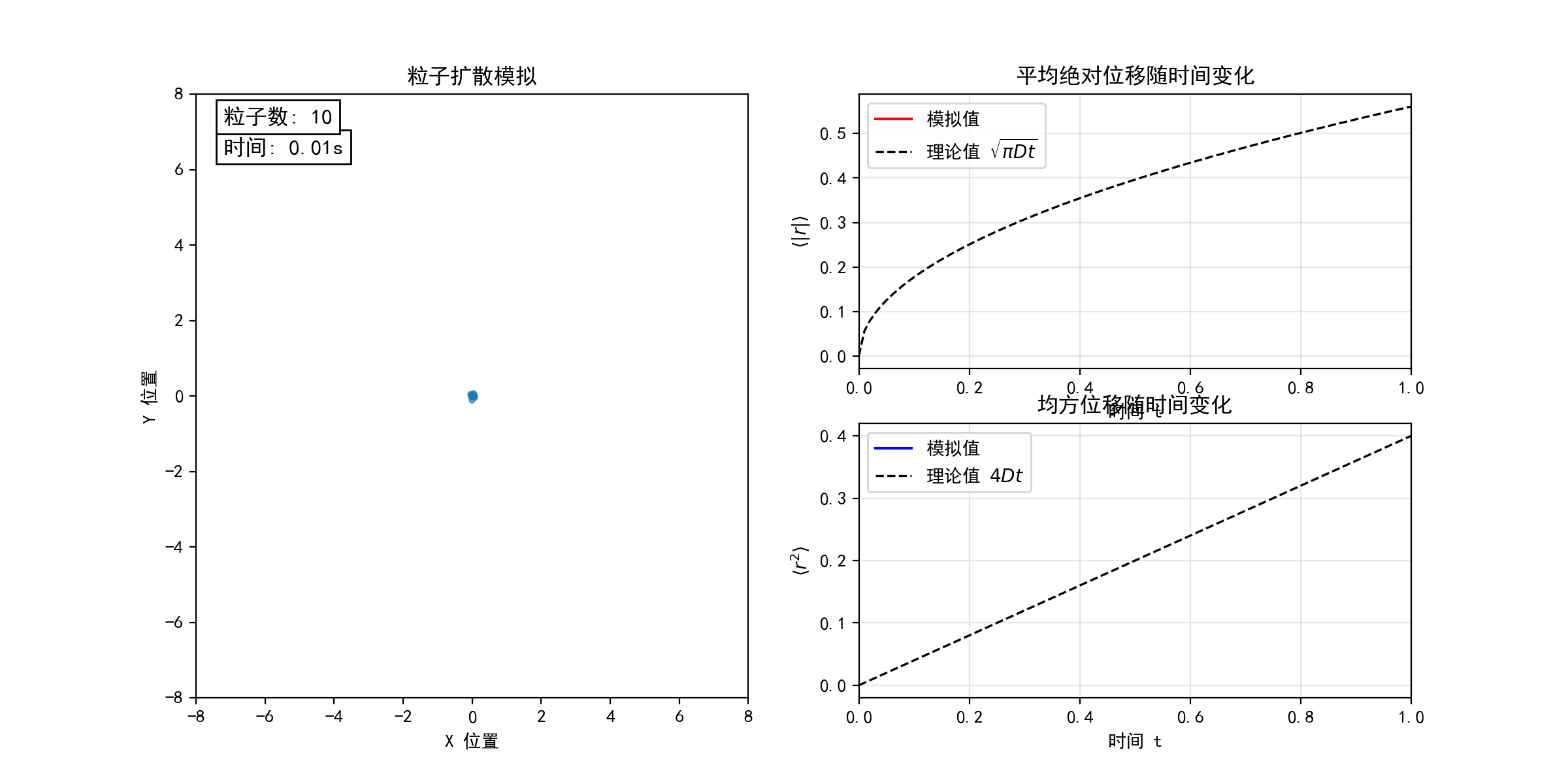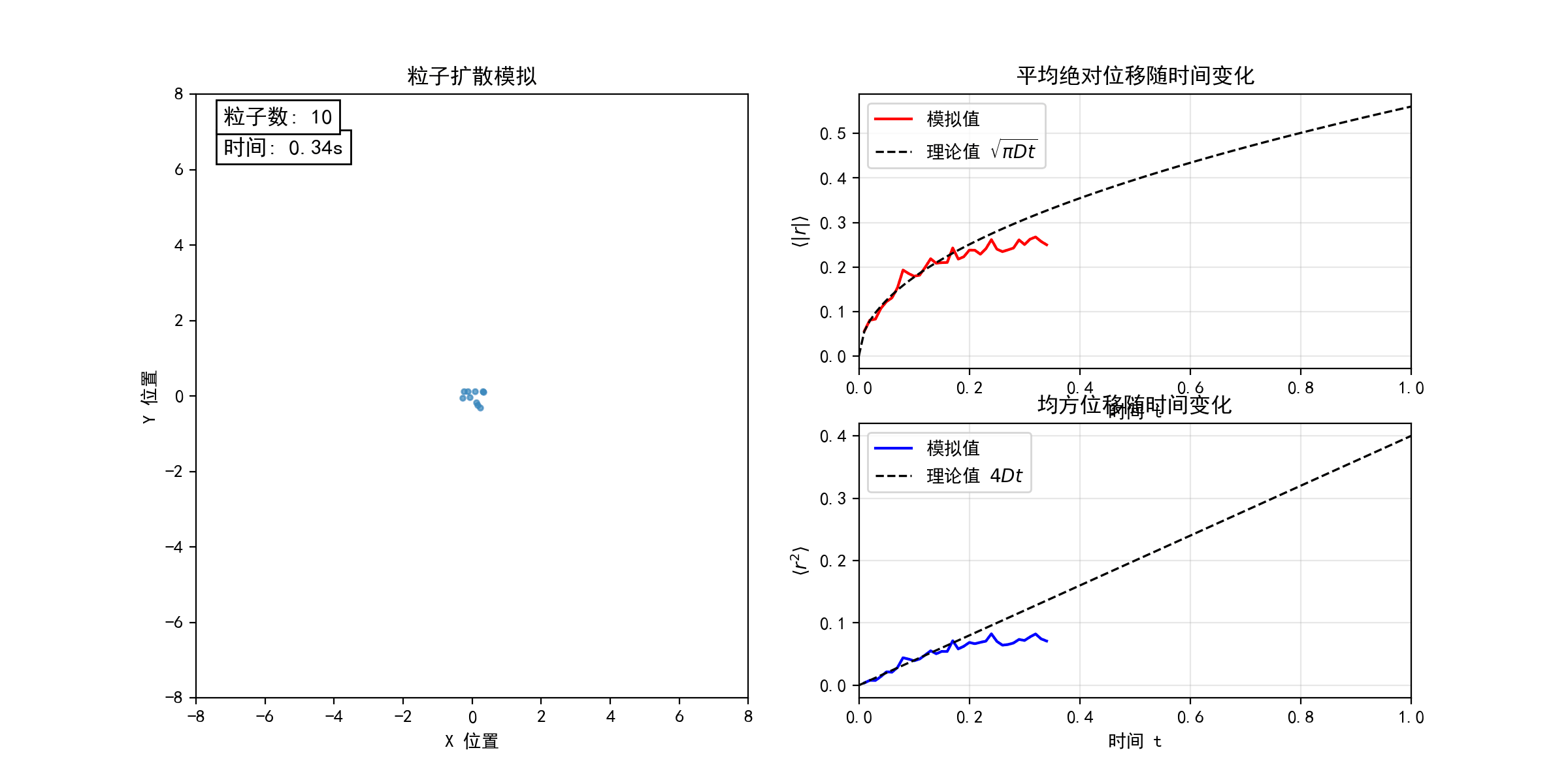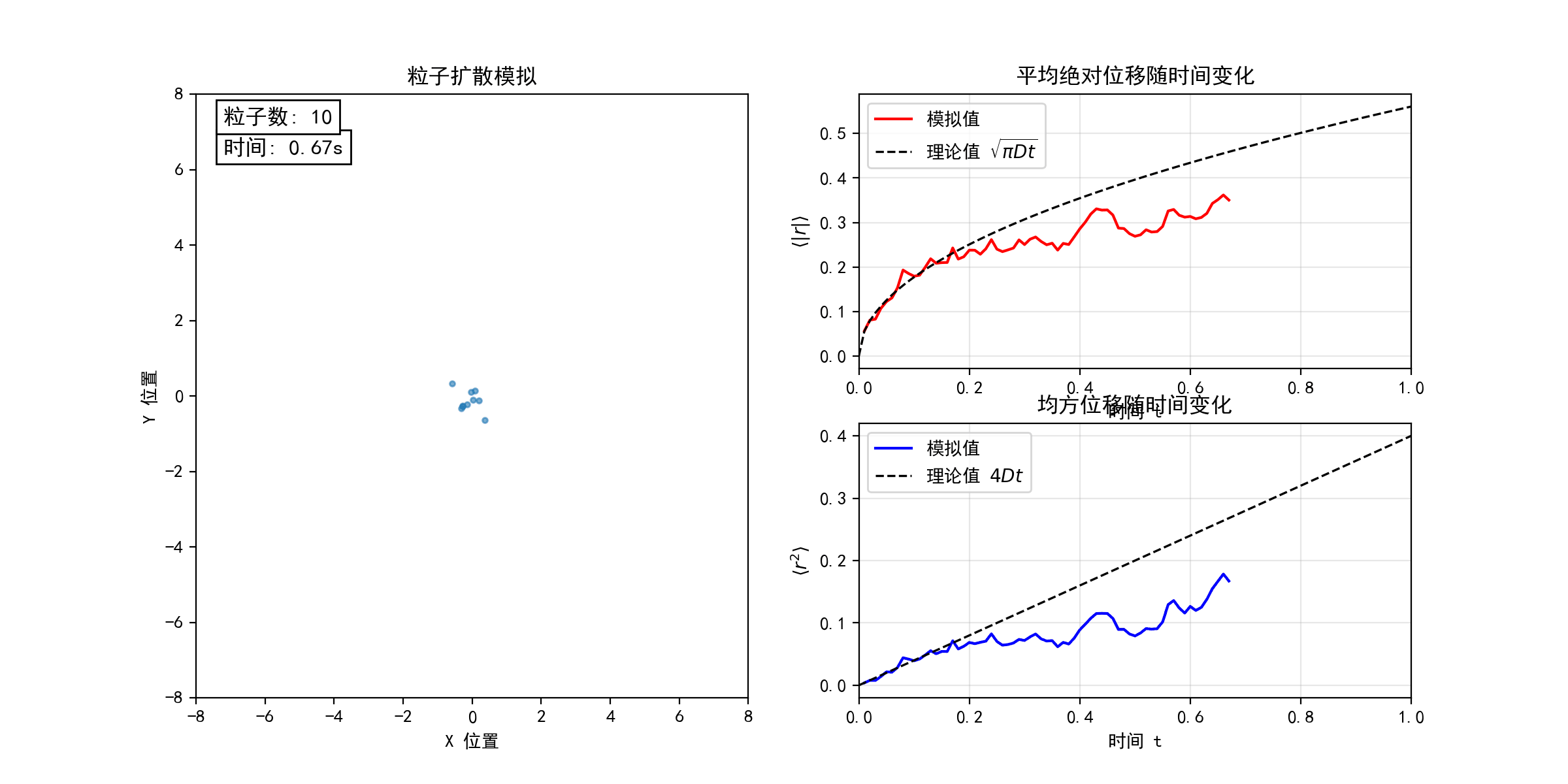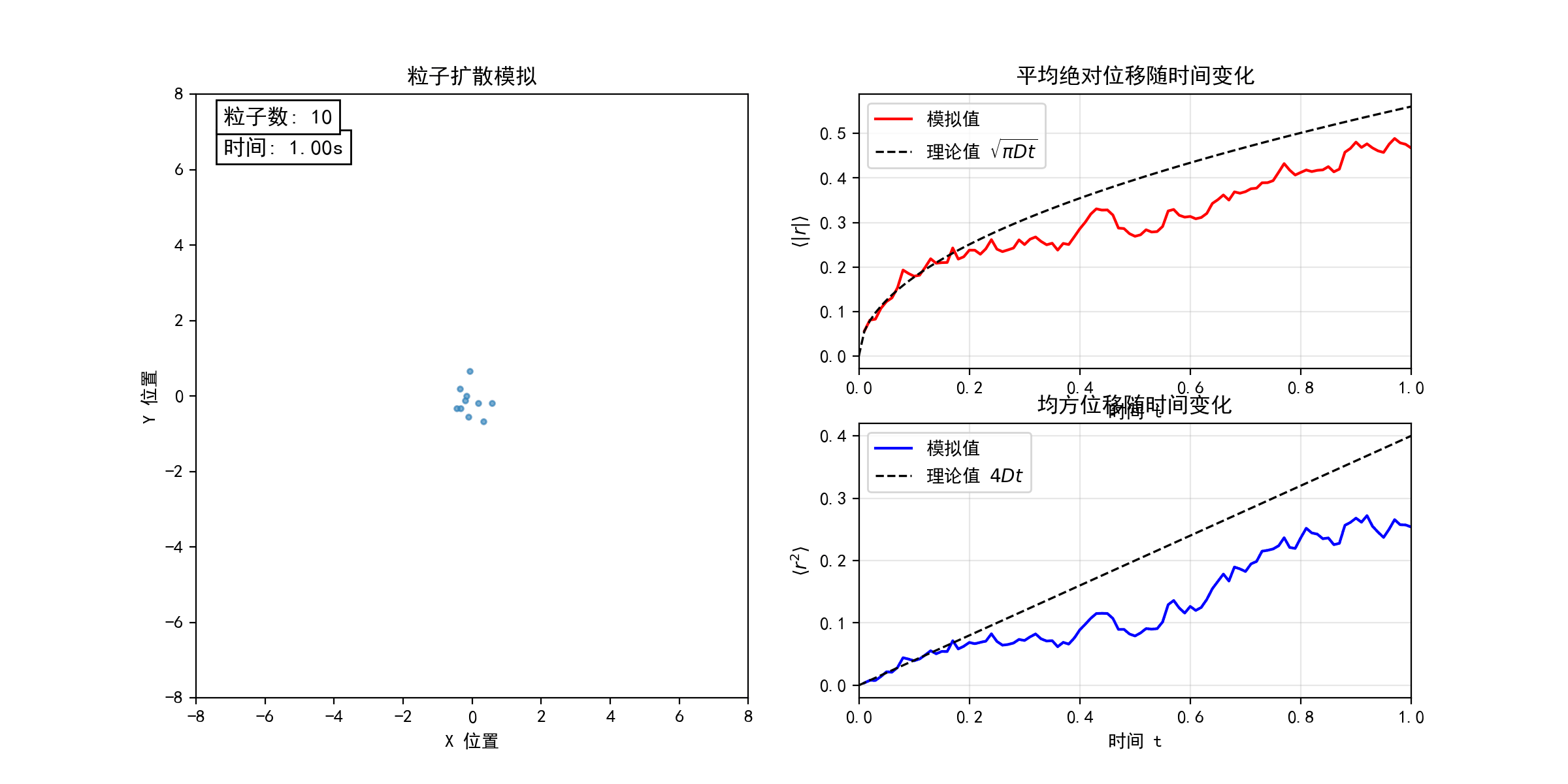
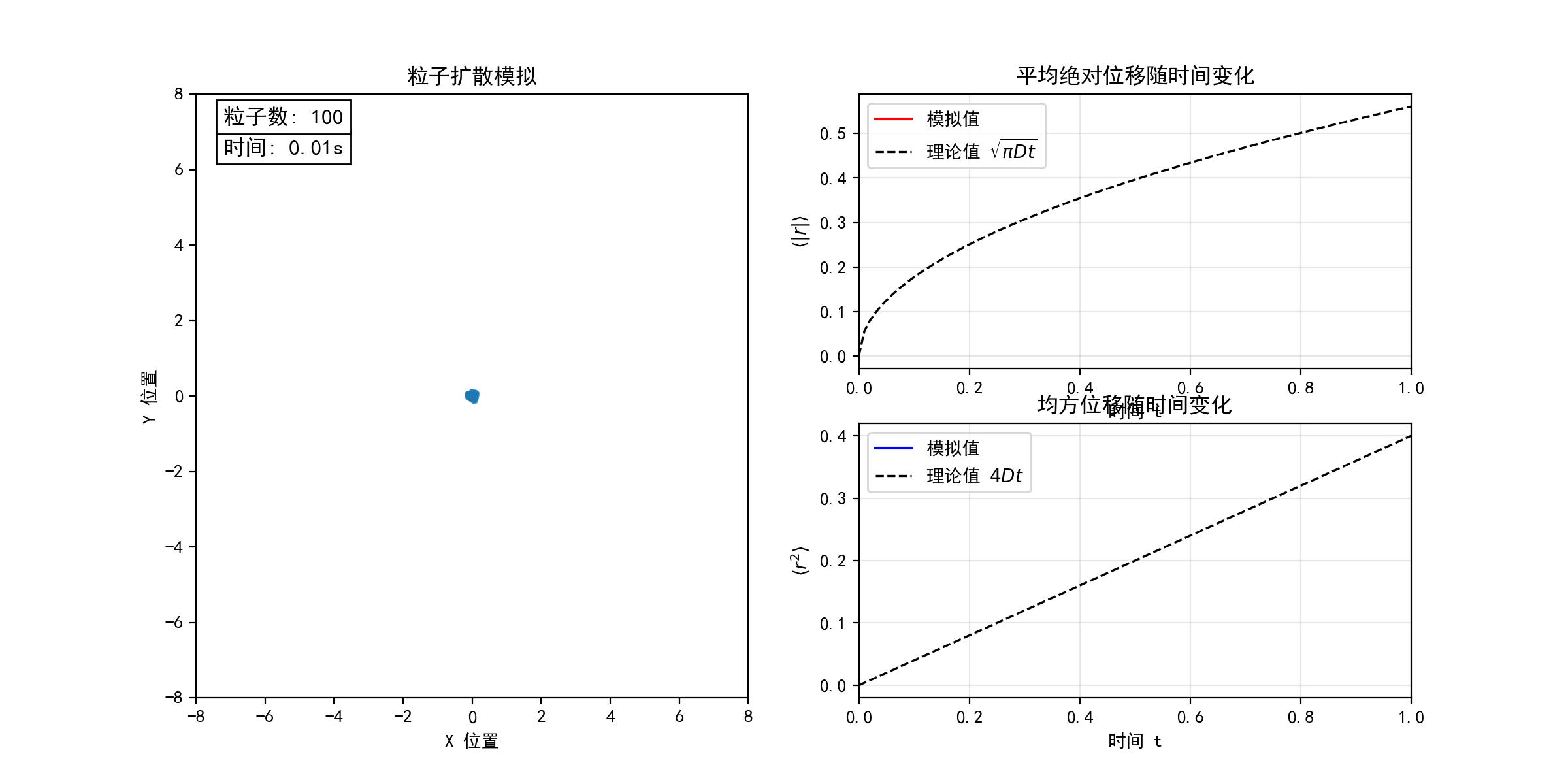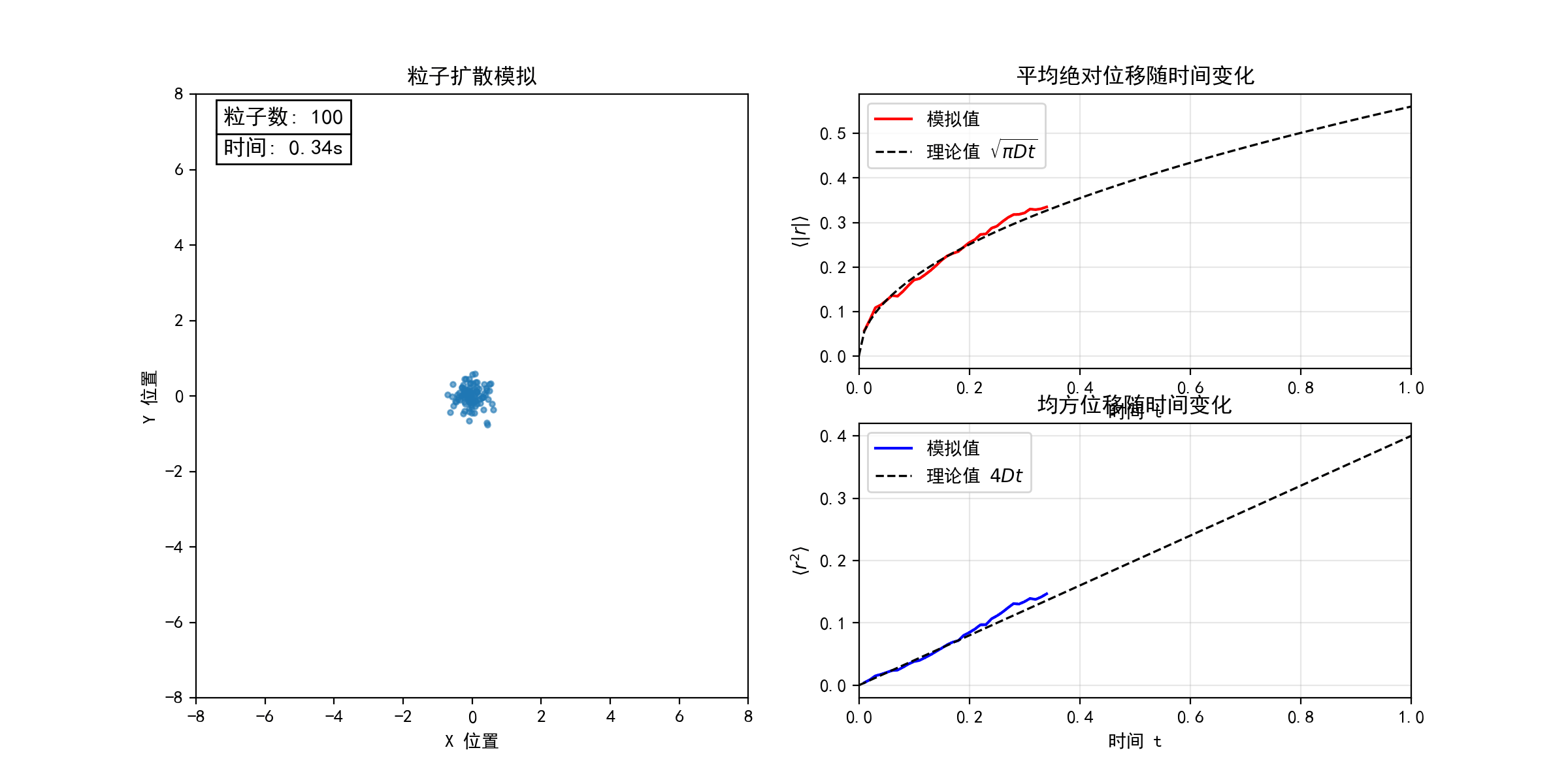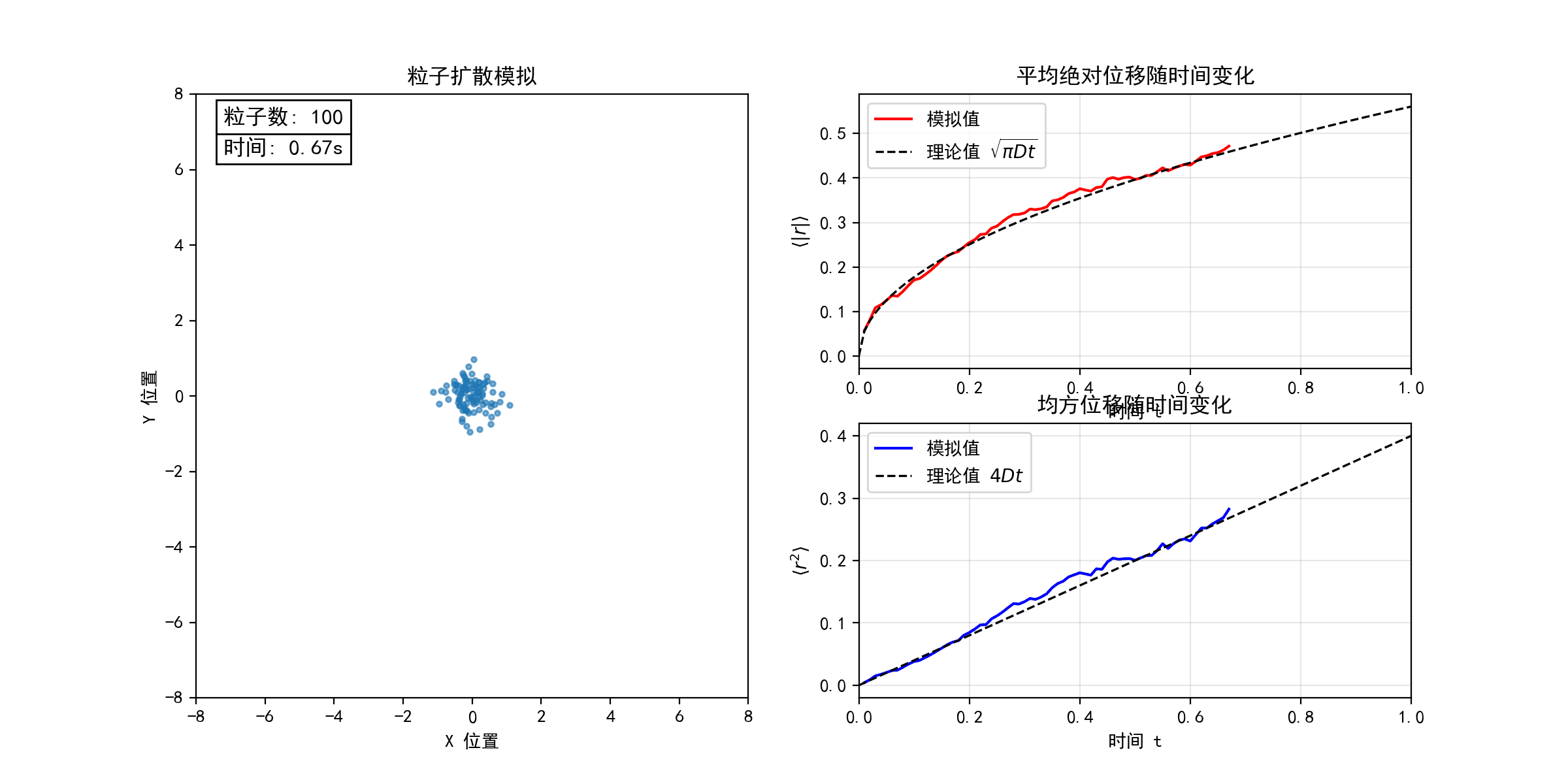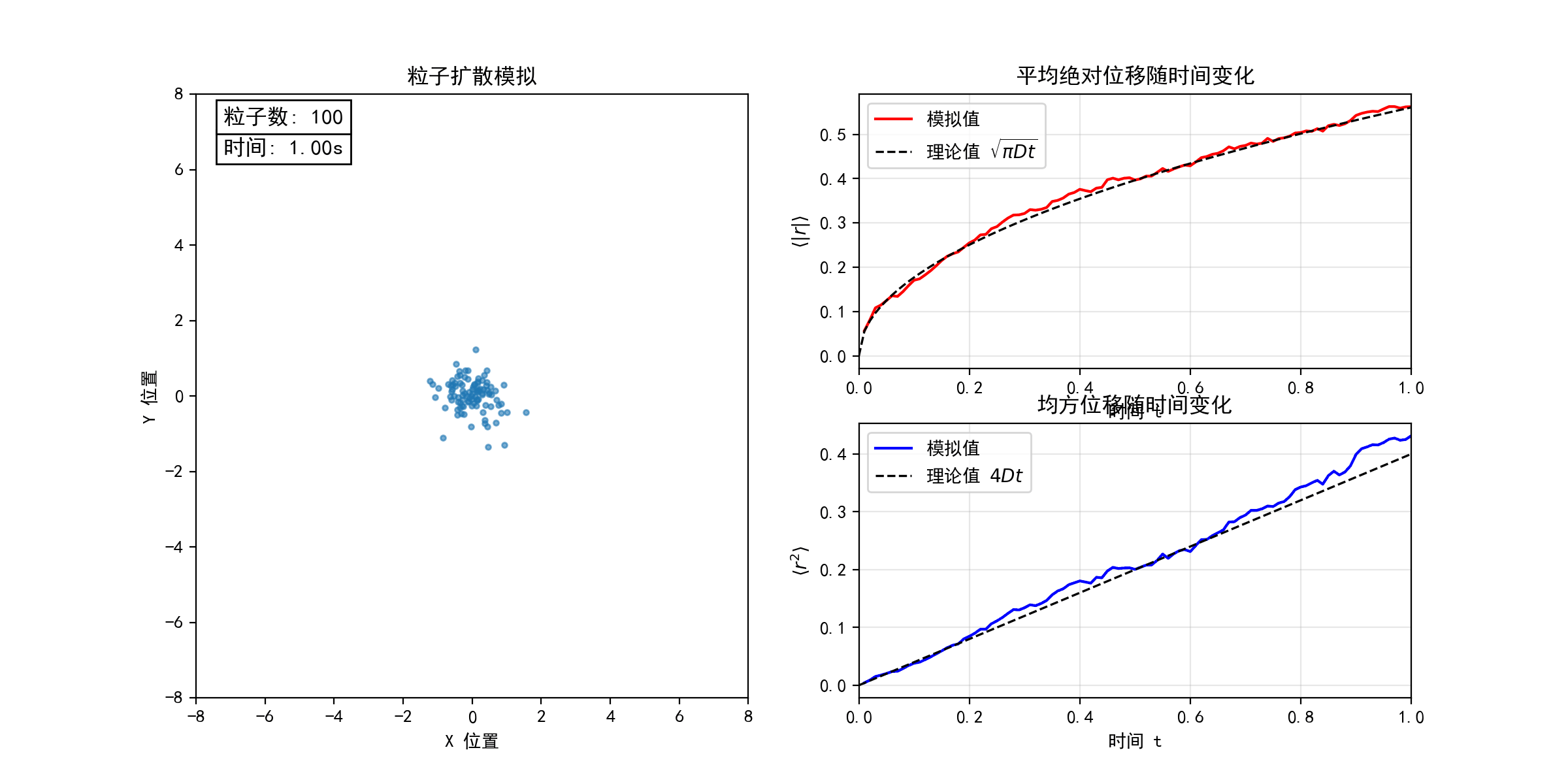
考虑一滴墨水在水中的扩散过程。初始时,墨汁颗粒聚集于容器左侧,因水分子撞击而做布朗运动。由于颗粒间存在体积排斥作用,它们的运动并非完全独立,而是相互制约的随机行走。为简化建模,考虑 N 个粒子(图中黑点)初始集中于边长为L的正方形区域左侧,每个粒子以等概率向四个方向随机移动(目标格点需未被其他粒子占据)。
从宏观角度来看,粒子将逐渐向右扩散,密度分布 ρ(x) 从初始的δ函数渐演化均匀分布。若定义 t 时刻第 x 列的粒子数为 Nx(t),则作为宏观可观测量的粒子密度分布为 ρ(x,t)=Nx(t)/L。系统对应的微观状态数为 ,相应的Boltzmann熵为 S(t) = kB ln Ω(t)。
当 t → ∞ 时,粒子达到完全均匀分布,此时 Nx = N/L,可以根据上面公式计算出相应的状态数 Ω0 和熵 S0,模拟结果展示了熵随时间单调增长的过程,并在 t → ∞ 时渐近趋近于虚线表示的平衡态熵值。
图中的模拟参数为 N=20 和 L=10。初始时刻状态数Ω=1,熵为0;虚线对应平衡态状态数 Ω0 = 34050628916015625 ≈ 3.4 × 1016,熵 S0 = kB ln Ω0 ≈ 38kB。(python代码下载)
与Boltzmann和Maxwell同为统计力学的创建者。建立系综理论,发明“统计力学”的名称。与Heaviside独立发展现代向量分析理论。
Einstein: "the greatest mind in American history"
美国本土第五个博士,第一个工程学博士(学位论文《论直齿轮轮齿的样式》)。父亲是耶鲁大学神学院教授。出生在耶鲁大学(New Haven),本科毕业于耶鲁大学,博士毕业于耶鲁大学,留校当助教,前两年讲授拉丁语,后面讲授物理,1871年获得数学物理教职,但因没有论文很快被辞退,住在妹妹家,没有工资收入10年,在耶鲁大学当教授,去世后墓地的在耶鲁大学(New Haven)。1873年,34岁的吉布斯开始发表学术论文。在耶鲁大学前10年没有工资,直到John Hopkins用3000美元一年聘请,耶鲁大学用2000美元一年将他留下。
Lord Rayleigh(氩气,黑体辐射): Gibbs' book was "too condensed and too difficult for most, I might say all, readers". Gibbs wrote back saying the book was only "too long".
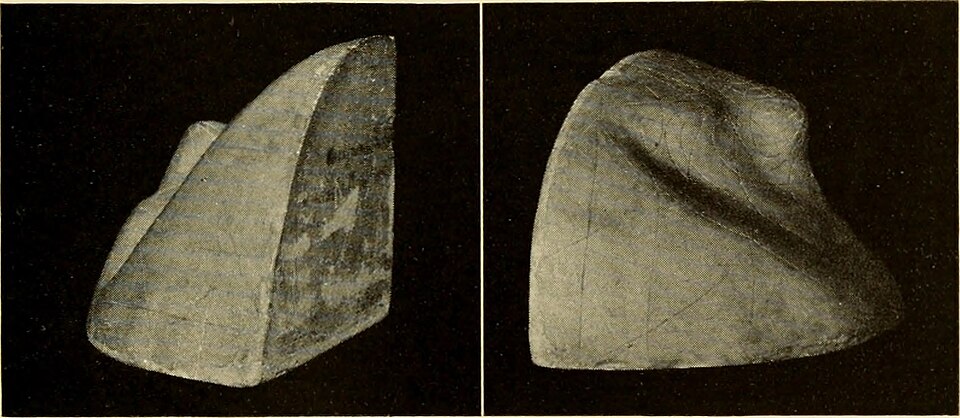
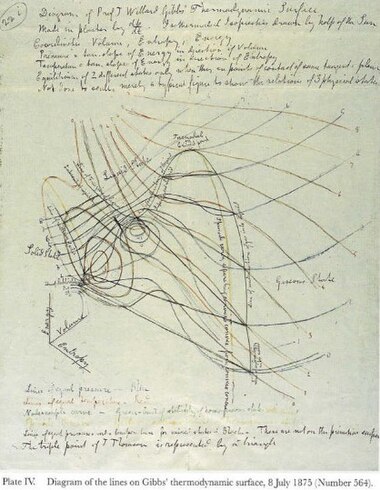
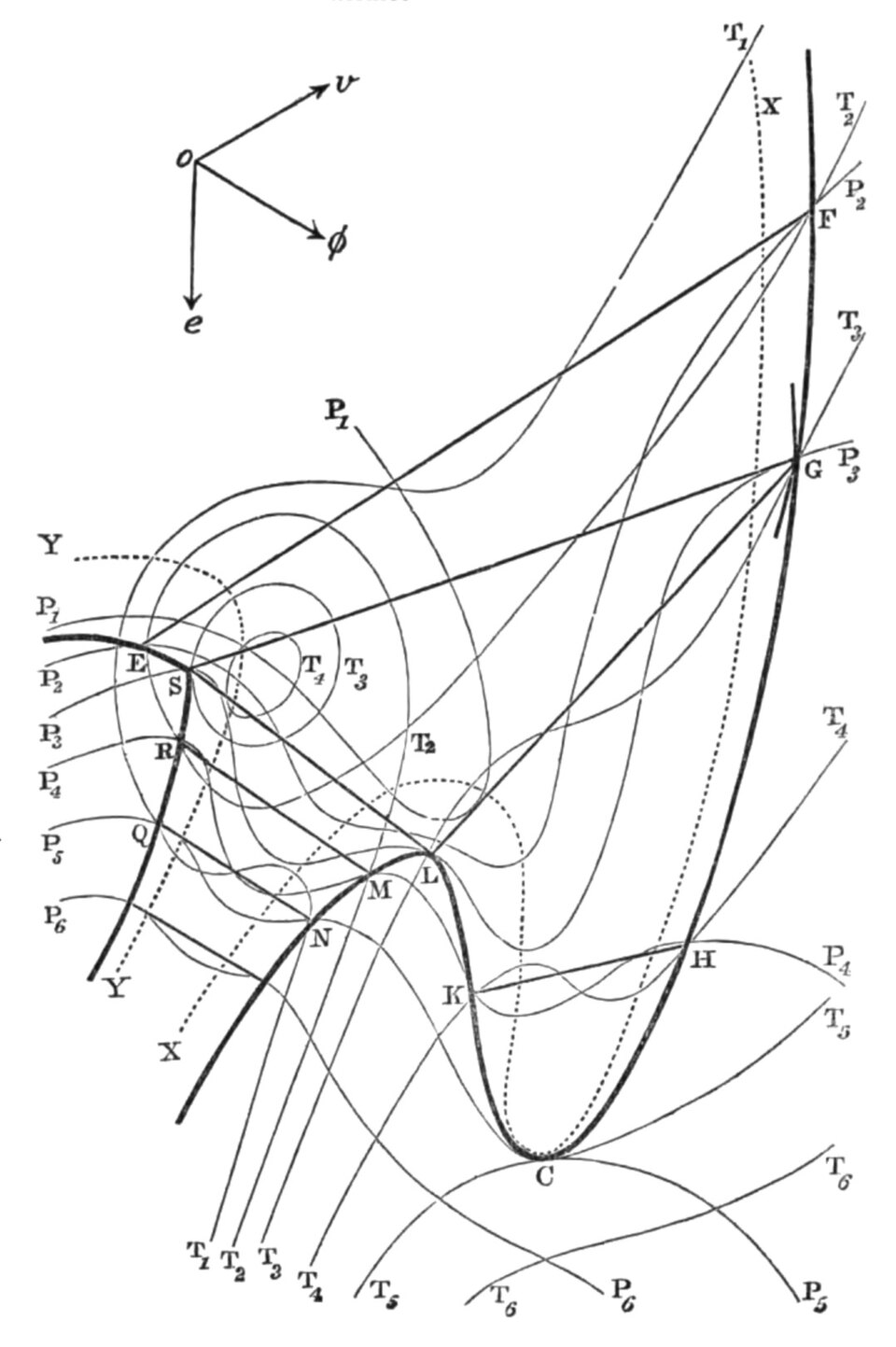
Maxwell's thermodynamic surface of U-V-S


宇宙微波背景(CMB, Cosmic Microwave Background)是宇宙起源大爆炸理论的标志性证据。在大爆炸早期,宇宙充满了一层不透明的浓密、炽热的亚原子粒子等离子体迷雾。随着宇宙膨胀,这些等离子体冷却到约 3000 K,质子和电子结合形成以氢为主的中性原子,光子与物质解耦,宇宙变得透明,从而在宇宙中留下一个几乎均匀的背景辐射场。
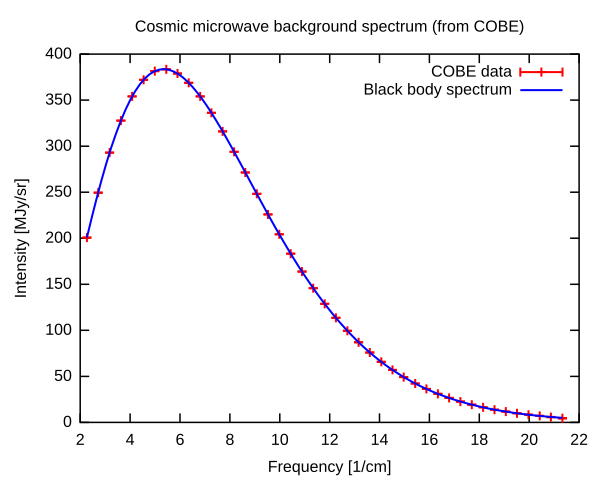
CMB的能谱是迄今为止测量到的最完美的黑体谱,对应温度为2.72548 ± 0.00057 K。(宇宙膨胀使得温度降低,否则夜空将会像太阳一样亮。)空间方向涨落约为 25000 分之一。
CMB 以 400 比 1 的比例,拥有宇宙中绝大多数的光子。CMB 中光子数密度是宇宙中物质数密度的十亿倍。